Consider a complicated dynamical system such as a litre of gas or a turbulent fluid, which has many more degrees of freedom than we can possibly track. Our knowledge might be limited to measurements at a few points in space, for example. Entropy is a measure of disorder which gauges the deficit of information between complete knowledge of the system and our observational knowledge.
To quantify entropy, consider a phase space Y having one axis for each degree of freedom. Phase space points correspond to exact states of the system, and trajectories to its temporal evolution. If knowledge is not exact, we can characterize possible states by a probability distribution p.
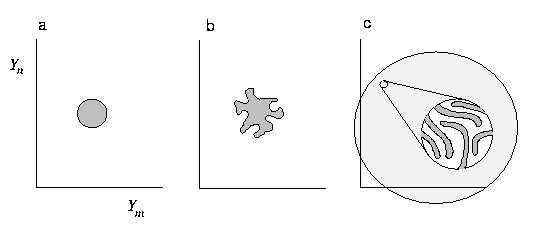
The figure below illustrates evolution of p for a complex system. Two of the many phase space dimensions are shown. We assume that initial conditions are sufficiently well known that initial p is somewhat localized (a).

As the system evolves, p is stretched and deformed (b). Eventually p fills accessible phase space and becomes so intricate that observations can no longer resolve its structure (c).
To quantify this process, we divide phase space into N cells whose sizes are determined by our ability to observe the system. We represent p by a random sample of n realizations, where n is sufficiently large that the finest structures in p are evident:

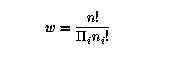
Because there are w possible p for each P, the information
deficit of P relative to p is

were S is the entropy, and k determines the units in which S is measured:
for S in bits, k= 1/log 2. To express S in terms of P, we apply
Stirling's approximation log ni! = ni
log ni - ni for large ni,
which yields
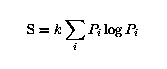
where we have divided by n to obtain the entropy per realization.
It is easily seen that S measures the concentration of P. If P is concentrated in one cell (maximal organization), then S=0. (The approximation that yields the second expression for S above then breaks down.) If P is distributed uniformly among all N accessible cells (maximal disorganization), then S attains a maximum value of k log N-1.
In general, systems that are sufficiently complex ("chaotic") and evolve conservatively under their internal dynamics approach states of maximum entropy. This is essence of Boltzmann's H theorem and the second law of thermodynamics.
See: Entropy gradient forcing -- a simple example orto Planetwater |
 |
or | more research |
 |
This page reflects contribution from Bill Merryfield.
Dysfonction érectile or